Verschil tussen Power Series en Taylor Series
Power Series vs Taylor Series
In wiskunde is een echte sequentie een bestelde lijst met echte getallen. Formeel is het een functie van de set van natuurlijke getallen in de set van echte getallen. Als a n de n th term van een reeks is, wijzen we de sequentie aan of door a 1 , a 2 , …, a n, …. Overweeg bijvoorbeeld de volgorde 1, ½, ⅓, …, 1 / n , …. Het kan worden aangeduid als {1 / n}.
Het is mogelijk om een serie te definiëren met behulp van sequenties. Een serie is de som van de termen van een sequentie. Daarom is er voor elke sequentie een bijbehorende sequentie en omgekeerd. Als {a n} de sequentie onder overweging is, dan kan de reeks die door die sequentie wordt gevormd, worden weergegeven als:
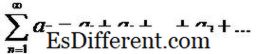
Dus in het bovenstaande voorbeeld is de bijbehorende serie 1+ 1 / 2 + 1 / 3 + … + 1 / n + ….
Zoals de namen suggereren, is de power-serie een speciaal type serie en wordt het uitgebreid gebruikt in numerieke analyse en verwante wiskundige modellering. Taylor-serie is een speciale power-serie die een alternatieve en makkelijk te manipuleren manier biedt om bekende functies te vertegenwoordigen.
Wat is Power series?
Een power-serie is een serie van het formulier
, die convergent is (mogelijk) voor een interval dat centraal staat op c. De coëfficiënten a n kunnen echt of complexe getallen zijn en is onafhankelijk van x; ik. e. de dummy-variabele.
Als u bijvoorbeeld a n = 1 voor elk n, en c = 0 instelt, wordt de vermogensreeks 1 + x + x 2 + … + x n + … is verkregen. Het is gemakkelijk te observeren dat wanneer x ε (-1, 1) deze power-serie convergeert naar 1 / (1-x).
Een power-serie convergeert wanneer x = c. De andere waarden van x waarvoor de vermogensreeks convergeert, heeft altijd de vorm van een open interval dat centraal staat op c. dat is, er zal een waarde 0 < R ≤ ∞ zijn zodat voor elke x bevredigende | xc | ≤ R, is de krachtreeks convergent en voor elke x bevredigende | xc |> R is de vermogensreeks afwijkend. Deze waarde R heet de convergentieradius van de krachtreeks (R kan elke echte waarde of positieve oneindigheid nemen).
Dan,
i. e.
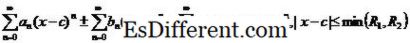
Wat is Taylor-serie? Taylor-serie is gedefinieerd voor een functie
f
(x) die oneindig differentieerbaar is op een interval. Stel dat f (x) differentieerbaar is op een interval dat centraal staat op c. Dan is de krachtreeks die wordt gegeven door
(x) over c. (hier f (n) (c ) noemen het n th derivaat bij x = c). In Numerische Analyse wordt een eindige aantal termen in deze oneindige uitbreiding gebruikt bij het berekenen van waarden op punten waar de serie convergerend is naar de oorspronkelijke functie. Er wordt in de interval (a, b) een functie f genoemd), als voor elke x e (a, b) convergeert de Taylor-serie f (x) naar de functie f (x). Bijvoorbeeld is 1 / (1-x) analytisch op (-1, 1), aangezien de Taylor-uitbreiding 1 + x + x 2 + … + x n + … convergeert naar de functie op dat interval en e x is overal analytisch, omdat de Taylor-serie e x converteert naar e x < voor elk echt getal x. Wat is het verschil tussen Power-serie en Taylor-serie? 1. Taylor-serie is een speciale klasse power series die alleen gedefinieerd is voor functies die oneindig differentieerbaar zijn op een bepaald open interval. 2. Taylor-serie neemt het speciale formulier, terwijl een krachtreeks elke serie van het formulier
