Verschil tussen integratie en summatie: integratie vs summatie vergeleken

Integratie vs Summation

In wiskunde, integratie en summatie worden bovenstaande wiskunde vaak gevonden in wiskundige operaties. Ze worden schijnbaar gebruikt als verschillende instrumenten en in verschillende situaties, maar ze delen een zeer nauwe relatie.

Meer over Summation

Summation is de werking van het toevoegen van een reeks getallen en de operatie wordt vaak aangeduid met de Griekse brief van hoofdstad sigma Σ. Het wordt gebruikt om de summatie te verkorten en gelijk aan de som / totaal van de sequentie. Ze worden vaak gebruikt om de serie te vertegenwoordigen, die in wezen oneindige sequenties samengevat zijn. Ze kunnen ook gebruikt worden om de som van vectoren, matrices of polynomen te geven.

De summatie wordt meestal gedaan voor een reeks waarden die kunnen worden weergegeven door een algemene term, zoals een serie die een gemeenschappelijke term heeft. Het beginpunt en het eindpunt van de summatie staan ​​respectievelijk bekend als de ondergrens en de bovenste grens van de summatie.

Bijvoorbeeld, de som van de sequentie a ₁ , a ₂ , a ₃ , a ₄ , …, een _n is een ₁ + a ₂ + a ₃ + … + a _n die gemakkelijk kan worden weergegeven gebruik maken van de opsommingsnotatie als Σ ⁿ _{i = 1} a _i ; ik heet de index van summatie.

Veel variaties worden gebruikt voor de summatie op basis van de applicatie. In sommige gevallen kan de bovenste en ondergrens worden gegeven als een interval of een bereik, zoals Σ _1≤i≤100 a _i en Σ _{i∈ [1, 100]} a _i . Of het kan worden gegeven als een set van cijfers zoals Σ _i∈P a _i , waar P een gedefinieerde set is.

In sommige gevallen kunnen twee of meer sigma tekens gebruikt worden, maar ze kunnen als volgt worden genummerd; Σ _j Σ _k a _jk = Σ _{j, k} a _jk .

Ook volgt de opsomming veel algebraïsche regels. Aangezien de ingebedde operatie de toevoeging is, kunnen veel van de algemene regels van algebra toegepast worden op de sommen zelf en voor de afzonderlijke termen die door de opsomming worden weergegeven.

Meer over Integratie

De integratie wordt gedefinieerd als het omgekeerde proces van differentiatie. Maar in zijn geometrische weergave kan het ook worden beschouwd als het gebied dat wordt omsloten door de curve van de functie en de as. Daarom geeft de berekening van het gebied de waarde van een bepaald integraal, zoals aangegeven in het diagram.

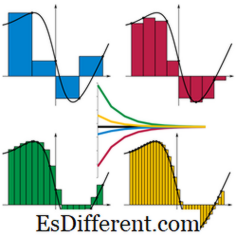
Beeldbron: // nl. wikipedia. org / wiki / Bestand: Riemann_sum_convergence. png

De waarde van het bepaalde integraal is eigenlijk de som van de kleine stroken in de kromme en de as.Het gebied van elke strook is de breedte × breedte op het punt op de overgelegde as. Breedte is een waarde die we kunnen kiezen, zeg Δx. En de hoogte is ongeveer de waarde van de functie op het overwogen punt, zeg f (x _i ). Uit het diagram blijkt dat hoe kleiner de strips beter zijn, passen de strips binnen het begrensde gebied, dus een betere benadering van de waarde.

Dus, in het algemeen, het bepaalde integraal I, tussen de punten a en b (i. E in het interval [a, b] waar a 1 ) Δx + f (x ₂ ) Δx + ⋯ + f n _{) Δx, waarbij n het aantal strips is (n = (ba) / xx). Deze summatie van het gebied kan gemakkelijk worden weergegeven met behulp van de opsommingsnotatie als} I ≅ Σ < n i = 1 ^f _(x i) Δx. Aangezien de approximatie beter is als Δx kleiner is, kunnen we de waarde berekenen als Δx → 0 Daarom is het redelijk om te zeggen _I = lim Δx → 0 Σ _n i = 1 ^f _(x i) Δx. _{Als algemene uit het bovenstaande begrip kunnen we de Δx kiezen op basis van het beschouwde interval geïndexeerd door i (de breedte van het gebied op basis van de positie kiezen). Dan krijgen we < I} = lim

Δx → 0

Σ n _{i = 1} f ^(x _i ) Δx i = _a ∫ _b f _{(x) dx} Dit staat bekend als de Reimann Integral van de functie ^f (x) in het interval [a, b]. In dit geval staan ​​a en b bekend als de bovenste en onderste grens van het integraal. Reimann integral is een basisvorm van alle integratiemethoden. In essentie is integratie de summatie van het gebied wanneer de breedte van de rechthoek oneindig is.

Wat is het verschil tussen Integratie en Summation? • Samenvatting is het opmaken van een reeks getallen. Meestal wordt de opsomming gegeven in deze vorm Σ n

i = 1

a

i ^{wanneer de termen in de reeks een patroon hebben en uitgedrukt kunnen worden met een algemene term.} _{• Integratie is in principe het gebied begrensd door de curve van de functie, de as en de bovenste en onderste grenzen. Dit gebied kan worden gegeven als som van veel kleinere gebieden in het begrensde gebied.} • Summatie omvat de discrete waarden met de bovenste en onderste grenzen, terwijl de integratie voortdurende waarden omvat. _{• Integratie kan worden geïnterpreteerd als een speciale vorm van summatie.} • In numerieke berekeningsmethoden wordt integratie altijd uitgevoerd als een samenvatting.