Verschil tussen Parallelogram en Vierhoek: Parallelogram vs Quadrilateral

parallellogram vs Quadrilateral < Vierhoeken en parallelogrammen zijn veelhoeken gevonden in de Euclidische Meetkunde. Parallelogram is een speciaal geval van de vierhoek. Vierhoeken kunnen zowel platte (2D) of 3-dimensionale zijn, terwijl parallelogrammen altijd planaire zijn.

Vierhoek

Vierhoek is een veelhoek met vier kanten. Het heeft vier hoekpunten en de som van de inwendige hoeken is 3600 (2π rad). Vierhoeken worden ingedeeld in zelfkruisende en eenvoudige vierhoekige categorieën. De zelfkruisende vierhoeken hebben twee of meer kanten elkaar overschreden, en kleinere geometrische figuren (zoals driehoeken worden gevormd binnen de vierhoek).

De eenvoudige vierhoeken worden ook verdeeld in convexe en concave vierhoeken. Concave vierhoeken hebben aangrenzende zijden die reflexhoeken in de figuur vormen. De eenvoudige vierhoeken die geen inwendige invalshoeken hebben, zijn convexe vierhoeken. De convexe vierhoeken kunnen altijd tessellaties hebben.

Een belangrijk deel van de geometrie van vierhoeken op de initiële niveaus betreft de convexe vierhoeken. Sommige quadrilaterals zijn ons zeer bekend uit de dagen van de basisscholen. Hierna volgt een diagram met verschillende convexe vierhoeken.

Parallelogram

Parallelogram kan worden gedefinieerd als de geometrische figuur met vier kanten, met tegengestelde zijden evenwijdig aan elkaar. Meer precies is het een vierhoek met twee parallelle kanten. Deze parallelle aard geeft veel geometrische kenmerken aan de parallelogrammen.

Een vierhoek is een parallelogram als er volgende geometrische eigenschappen worden gevonden.

• Twee paar tegenover elkaar gelegen zijden zijn even lang. (AB = DC, AD = BC)

• Twee paar tegengestelde hoeken zijn even groot. ()

• Als de aangrenzende hoeken aanvullend zijn

• Een paar zijden die elkaar tegengaan, zijn evenwijdig en gelijk in lengte. (AB = DC & ABIDEDC)

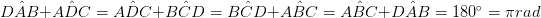
• De diagonalen scheiden elkaar (AO = OC, BO = OD)

• Elk diagonaal verdeelt de vierhoek in twee congruente driehoeken. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Verder is de som van de vierkanten van de zijkanten gelijk aan de som van de vierkantjes van diagonalen. Dit wordt soms aangeduid als de

parallelogram wet en heeft veelgebruikte toepassingen in natuurkunde en techniek. (AB 2 ^{+ BC} 2 ^{+ CD} 2 ^{+ DA} 2 ^{= AC} 2 ^{+ BD} 2 ⁾ Elk van de bovenstaande kenmerken kan worden gebruikt als eigenschappen, zodra er is vastgesteld dat de vierhoek een parallelogram is.

Gebied van het parallelogram kan berekend worden door het product van de lengte van de ene kant en de hoogte naar de tegenovergestelde kant. Daarom kan het gebied van het parallelogram worden aangegeven als

Gebied van parallelogram = basis × hoogte =

AB × h Het gebied van het parallelogram is onafhankelijk van de vorm van afzonderlijk parallelogram. Het is alleen afhankelijk van de lengte van de basis en de loodrechte hoogte.

Als de zijden van een parallelogram door twee vectoren kunnen worden weergegeven, kan het gebied worden verkregen door de grootte van het vectorproduct (kruisproduct) van de twee aangrenzende vectoren.

Als zij AB en AD zijn vertegenwoordigd door respectievelijk vectoren () en (

), wordt het gebied van het parallelogram gegeven door

, waarbij α de hoek is tussen

en.

Hieronder volgen enkele geavanceerde eigenschappen van het parallelogram;

• Het gebied van een parallelogram is tweemaal het gebied van een driehoek die door een van zijn diagonalen wordt gemaakt.

• Het gedeelte van het parallelogram is in de helft verdeeld door een lijn die door het middelpunt loopt.

• Een niet-gedegenereerde affine transformatie neemt een parallelogram naar een ander parallelogram

• Een parallelogram heeft rotatiesymmetrie van volgorde 2

• De som van de afstanden van een binnenpunt van een parallelogram aan de zijkanten is onafhankelijk van de plaats van het punt

Wat is het verschil tussen Parallelogram en Vierhoek?

• Vierhoeken zijn polygonen met vier zijden (soms tetragonen genoemd), terwijl parallelogram een ​​speciaal type vierhoek is.

• Vierhoeken kunnen hun zijden hebben in verschillende vlakken (in 3d-ruimte), terwijl alle zijden van het parallelogram op hetzelfde vlak liggen (vlak / 2-dimensionaal).

• Binnenhoeken van de vierhoek kunnen elke waarde (inclusief reflexhoeken) zodanig maken dat ze maximaal 3600 oplopen. Parallelogrammen kunnen alleen hoekige hoeken hebben als het maximale type hoek.

• Vier zijden van de vierhoek kunnen van verschillende lengtes zijn, terwijl de tegenover elkaar gelegen zijden van het parallelogram altijd evenwijdig aan elkaar zijn en gelijke lengte hebben.

• Elk diagonaal verdeelt het parallelogram in twee congruente driehoeken, terwijl de driehoeken die gevormd worden door het diagonaal van een algemene vierhoek niet noodzakelijkerwijs congruent zijn.