Verschil tussen differentiatie en derivaat

Differentiatie vs Derivaat

In differentiaalberekeningen zijn derivaten en differentiatie nauw verwant maar zeer verschillend en vertegenwoordigen ze twee belangrijke wiskundige concepten gerelateerd aan functies.

Wat is afgeleid?

Afleiden van een functie meet het tempo waarmee de functiewaarde verandert als de invoer verandert. Bij multivariabele functies hangt de verandering van de functiewaarde af van de richting van de verandering van de waarden van de onafhankelijke variabelen. Daarom wordt in deze gevallen een specifieke richting gekozen en wordt de functie in die bepaalde richting gedifferentieerd. Dat afgeleide wordt de richting afgeleide genoemd. Gedeeltelijke derivaten zijn een speciaal soort richtingderivaten.

Afgeleide van een vectorwaardewaarde f kan gedefinieerd worden als de limiet

waar het uiteindelijk bestaat. Zoals eerder vermeld, geeft dit ons de snelheid van toename van de functie f langs de richting van de vector u. In het geval van een enkele waarde, vermindert dit naar de bekende definitie van het afgeleide,

Bijvoorbeeld,

is overal differentieerbaar, en het afgeleide is gelijk aan de limiet,

, die gelijk is aan

. De derivaten van functies zoals

bestaan ​​overal. Ze zijn respectievelijk gelijk aan de functies

.

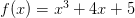
Dit is bekend als de eerste afgeleide. Meestal wordt het eerste afgeleide van functie f aangeduid door f ⁽¹⁾ . Met behulp van deze notatie is het mogelijk om hogere orderderivaten te definiëren.

is de tweede-orde-richtingderivaat en geeft het n ^th derivaat voor f ⁽ⁿ⁾ voor elke n,

, definieert het n ^th derivaat.

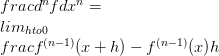
Wat is differentiatie?

Differentiatie is het proces van het vinden van het afgeleide van een differentieerbare functie. D-operator aangeduid met D vertegenwoordigt in bepaalde contexten differentiatie. Als x de onafhankelijke variabele is, dan D ≡ ^d / _dx . De D-operator is een lineaire operator, i. e. voor elke twee differentieerbare functie f en g en constant c, volgende eigenschappen vasthouden.

I. D (f + g) = D (f) + D (g)

II. D cD (f) Met behulp van de D-operator kunnen de andere regels die in verband staan ​​met differentiatie als volgt uitgedrukt worden. d

f g) = D (f) g D g) = < D ⁽ f _{) < g} - ^{en (g)] / g 2 en D (f} o _g ^{) = (} D (f) o g) D (g). Bijvoorbeeld, wanneer F (x) = x 2 sin x

is gedifferentieerd ten opzichte van x met behulp van de gegeven regels zullen het antwoord zijn x ^zonde x - + x 2 cos x. Wat is het verschil tussen differentiatie en derivaat? • Derivaat verwijst naar een veranderingssnelheid van een functie • Differentiatie is het proces om het afgeleide van een functie te vinden.