Verschil tussen derivaten en differentiaal

Derivaten vs Differentieel

In differentiaalberekeningen zijn derivaten en differentiaal van een functie nauw verwant maar hebben ze heel andere betekenissen en gebruikt om twee belangrijke wiskundige objecten in verband met differentieerbare functies te vertegenwoordigen.

Wat is afgeleid?

Afleiden van een functie meet het tempo waarmee de functiewaarde verandert als de invoer verandert. Bij multivariabele functies hangt de verandering van de functiewaarde af van de richting van de verandering van de waarden van de onafhankelijke variabelen. Daarom wordt in deze gevallen een specifieke richting gekozen en wordt de functie in die bepaalde richting gedifferentieerd. Dat afgeleide wordt de richting afgeleide genoemd. Gedeeltelijke derivaten zijn een speciaal soort richtingderivaten.

Afgeleide van een vectorwaardewaarde f kan gedefinieerd worden als de limiet

waar het uiteindelijk bestaat. Zoals eerder vermeld, geeft dit ons de snelheid van toename van de functie f langs de richting van de vector u. In het geval van een enkele waarde, vermindert dit naar de bekende definitie van het afgeleide,

Bijvoorbeeld,

is overal differentieerbaar, en het afgeleide is gelijk aan de limiet,

, die gelijk is aan

. De derivaten van functies zoals

bestaan ​​overal. Ze zijn respectievelijk gelijk aan de functies

.

Dit is bekend als de eerste afgeleide. Meestal wordt het eerste afgeleide van functie f aangeduid door f ⁽¹⁾ . Met behulp van deze notatie is het mogelijk om hogere orderderivaten te definiëren.

is de tweede-orde-richtingderivaat en geeft het n ^th derivaat voor f ⁽ⁿ⁾ voor elke n,

, definieert het n ^th derivaat.

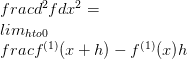
Wat is differentiaal?

Differentieel van een functie vertegenwoordigt de verandering in de functie met betrekking tot veranderingen in de onafhankelijke variabele of variabelen. In de gebruikelijke notatie wordt voor een bepaalde functie f van een enkele variabele x het totale verschil van orde 1 df gegeven door

. Dit betekent dat voor een oneindige verandering van x (x) een f ⁽¹⁾ (x <) d x verandering in f. Met limieten kan men deze definitie als volgt volbrengen. Veronderstel dat Δ

x de verandering in x op een willekeurig punt x en Δ f is de overeenkomstige verandering in de functie f. Het kan worden aangetoond dat Δ f = f (1) ⁽ x) Δ x + ε, waar ε is de fout. Nu, de limiet Δ x 0 Δ ^{f /} Δ _{x =} f (1) ^x ) > = 0.Daarom is het mogelijk om te concluderen dat Δ x → 0 ε = 0. Nu, aangeduid met Δ ^{x →} 0 Δ _{f zoals d} f en Δ x → 0 Δ x als d x wordt de definitie van het differentiaal streng verkregen. Bijvoorbeeld, het differentiaal van de functie is. In het geval van functies van twee of meer variabelen, wordt het totale verschil van een functie gedefinieerd als de som van verschillen in de richtingen van elk van de onafhankelijke variabelen. Mathematisch kan het worden aangegeven als. Wat is het verschil tussen afgeleide en differentiaal? • Derivaat verwijst naar een veranderingssnelheid van een functie, terwijl het differentiaal verwijst naar de feitelijke wijziging van de functie, wanneer de onafhankelijke variabele onderworpen is aan verandering. • Het afgeleide is gegeven door, maar het differentiaal wordt gegeven door

.