Verschil tussen Parallelogram en Rhombus: Parallelogram vs ruit

Parallelogram vs ruit

Parallellogram en rhombus zijn vierhoeken. De geometrie van deze figuren was duizenden jaren bekend. Het onderwerp wordt expliciet behandeld in het boek "Elements" geschreven door de Griekse wiskundige Euclid.

Parallelogram

Parallelogram kan worden gedefinieerd als de geometrische figuur met vier kanten, met tegengestelde zijden evenwijdig aan elkaar. Meer precies is het een vierhoek met twee parallelle kanten. Deze parallelle aard geeft veel geometrische kenmerken aan de parallelogrammen.

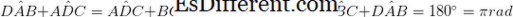
Een vierhoek is een parallelogram indien de volgende geometrische eigenschappen worden gevonden.

• Twee paar tegenover elkaar gelegen zijden zijn even lang. (AB = DC, AD = BC)

• Twee paar tegengestelde hoeken zijn even groot. (

)

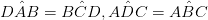
• Als de aangrenzende hoeken aanvullend zijn

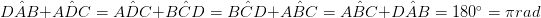
• Een paar zijden, die elkaar tegengaan, is parallel en gelijk in lengte. (AB = DC & ABIDEDC)

• De diagonalen scheiden elkaar (AO = OC, BO = OD)

• Elk diagonaal verdeelt de vierhoek in twee congruente driehoeken. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Verder is de som van de vierkanten van de zijkanten gelijk aan de som van de vierkantjes van diagonalen. Dit wordt soms aangeduid als de parallelogram wet en heeft veelgebruikte toepassingen in natuurkunde en techniek. (AB ² 2 ^{+ CD} 2 ^{+ DA} 2 ^{= AC} 2 ^{+ BD} 2 ⁾ Elk van de bovenstaande kenmerken kan worden gebruikt als eigenschappen, zodra er is vastgesteld dat de vierhoek een parallelogram is.

Gebied van het parallelogram kan berekend worden door het product van de lengte van de ene kant en de hoogte naar de tegenovergestelde kant. Daarom kan gebied van het parallelogram worden aangegeven als

Gebied van parallelogram = basis × hoogte = AB × h

Het gebied van het parallelogram is onafhankelijk van de vorm van het afzonderlijke parallelogram. Het is alleen afhankelijk van de lengte van de basis en de loodrechte hoogte.

Als de zijden van een parallelogram door twee vectoren kunnen worden weergegeven, kan het gebied worden verkregen door de grootte van het vectorproduct (kruisproduct) van de twee aangrenzende vectoren.

Als zij AB en AD zijn vertegenwoordigd door respectievelijk vectoren () en (

), wordt het gebied van het parallelogram gegeven door

, waarbij α de hoek is tussen

en.

Hieronder volgen enkele geavanceerde eigenschappen van het parallelogram;

• Het gebied van een parallelogram is tweemaal het gebied van een driehoek die door een van zijn diagonalen wordt gemaakt.

• Het gedeelte van het parallelogram is in de helft verdeeld door een lijn die door het middelpunt loopt.

• Een niet-gedegenereerde affine-transformatie heeft een parallelogram naar een ander parallellogram

• Een parallelogram heeft rotatiesymmetrie van volgorde 2

• De som van de afstanden van een binnenpunt van een parallelogram aan de zijkanten is onafhankelijk van de plaats van het punt

Rhombus

Een vierhoek met alle kanten gelijk is, staat bekend als een ruit. Het wordt ook genoemd als een

evenwijdige vierhoek

. Het wordt beschouwd als een diamantvorm, vergelijkbaar met die in de speelkaarten. Rhombus is ook een speciaal geval van het parallelogram. Het kan worden beschouwd als een parallelogram met alle vierzijden gelijk. En het heeft speciale eigenschappen, naast de eigenschappen van een parallelogram. • De diagonalen van de ruit baken elkaar in rechte hoeken; diagonalen zijn loodrecht.

• De diagonalen scherpen de twee tegenover elkaar gelegen inwendige hoeken.

• Tenminste twee van de naast elkaar gelegen zijden zijn gelijk aan lengte.

Het gebied van de ruit kan volgens dezelfde methode als het parallelogram worden berekend.

Wat is het verschil tussen Parallelogram en Rhombus?

• Parallelogram en rhombus zijn vierhoeken. Rhombus is een speciaal geval van de parallelogrammen.

• Gebied van elk kan worden berekend met behulp van de formulebasis × hoogte.

• Overweegt de diagonalen;

- De diagonalen van het parallelogram halveren elkaar en halveren het parallelogram om twee congruente driehoeken te vormen.

- De diagonalen van de ruit baken elkaar in rechte hoeken en de gevormde driehoeken zijn evenwijdig.

• Gezien de interne hoeken;

- Opperste invalshoeken van het parallelogram zijn gelijk aan grootte. Twee aangrenzende inwendige hoeken zijn aanvullend.

- De inwendige hoeken van de ruit worden door de diagonalen gesneden.

• gezien de zijkanten;

- In een parallelogram is de som van vierkanten van de zijkanten gelijk aan de som van de vierkantjes van het diagonaal (Parallelogramwet).

- Zoals alle vierzijden gelijk zijn in een ruit, is vier keer het vierkant van een kant gelijk aan de som van de vierkantjes van het diagonaal.